Summary
A dynamically coupled interface has been developed to determine the three-dimensional transient thermo-structural response of the hypersonic vehicle during its flight. Dynamic coupling is required when the change in aerothermal state, surface temperature, ablation, mass/momentum/energy transfer at the surface, and shape change of a hypersonic vehicle due to the thermal loading from the aerothermal environment couples with the structural solver. This results in a strong coupling between the two codes. The coupled codes are more accurate in modelling the interdisciplinary thermo-physico-chemical interactions compared to each separately simulated process. The dynamic coupling is achieved by a code-independent robust and agile python interface that utilizes a tree-based search algorithm to enable nonmatching mesh on the computational domains on the fluid and structural sides. This occurs when the mesh size and node position of the two domains are different and dynamically evolving due to displacement- and/or ablation-induced surface regression. The algorithm performs search associations to find the mesh nodes from both domains at the interface and data interpolations between nonmatching meshes for the quantities to map via the interpolation algorithm.
If there is no structural deformation that could affect the calculated flow, the next timestep will be run on the same structural mesh as earlier without any changes. This will allow the program to save time by not having to unnecessarily modify the mesh. In either case, the total grid count in the fluid or solid computational domains will not alter—only the grid will be adapted based upon structural deformations due to mass loss and/or thermo-structural response of the solid. A proof-of-concept of the interface has been developed in-house, and canonical results are shown.
Introduction
During flight, the hypersonic vehicle is subjected to aerodynamic thermal and mechanical loads transferred to its structure, including the vehicle’s thermal protection system. The combined thermal and mechanical loading results in increased surface temperatures, ablation, and mass/momentum/energy transfer at the surface of the hypersonic vehicle. There are two possibilities for the interface between the fluid and the vehicle’s outer mold line: (1) surface regression (due to ablation, weather erosion, and/or spallation) and (2) surface deformation (due to the aerodynamic forces exerted on the surface). Both phenomena affect the interface between the fluid and structural domains. To enable coupled, high-fidelity computational simulations of integrated aerothermal-material-structural response of the thermal-protection material (TPS) material when subjected to aerothermal heating, material ablation, and resulting shape change process, it is important to exchange information from both sides. Therefore, the grid deformation of the interface (which is a boundary for the fluid domain) must be determined.
This work aims at enabling high-fidelity simulation of integrated aerothermal-material-structural response of the TPS material when subjected to aerothermal heating, material ablation, and resulting shape change process. To achieve such close coupling, a modular and flexible interface was developed that can dynamically couple a three-dimensional (3-D), transient, aerothermal code with ablation and finite-element analysis codes. Dynamic coupling means that the change in aerothermal state, surface temperature, ablation, mass/momentum/energy transfer at the surface, and shape change of a hypersonic vehicle couple with the structural solver. This results in a strong coupling between the two codes. The coupled codes are more accurate in modelling the interdisciplinary thermo-physico-chemical interactions associated with an aerothermal flow, 3-D, transient, thermo-structural response of the TPS material while it undergoes shape change.
The dynamic data exchange interface presented in this article is code agnostic. It is developed as a modular stand-alone capability that can be used to perform data exchange between any CFD and structural codes without restrictions on whether they are structured or unstructured. A unique and innovative aspect of this code is its ability to maintain connectivity when the solid shape is changing because of ablation and structural deformation. The flexible interface can enable computational affordability for the coupled, high-fidelity simulations, as it will free the codes from the restriction of having a perfect match at the aerothermal-structural interface in the presence of shape change due to ablation and deformation. Therefore, the computationally affordable, dynamically coupled modelling and simulation capability will deliver an improved methodology for TPS design for hypersonic flight systems.
Objectives
The purpose of this research was to enable computational simulations of fully coupled fluid-structure phenomena by executing the following objectives:
- Develop the tree-based machine learning (ML) method for data exchange between structured and unstructured mesh, representing typical fluid and structural dynamics solvers, respectively.
- Conduct a demonstration to maintain the interface connectivity under multiple scenarios, including deformation and regression of the interface between the two mesh (i.e., structured and unstructured).
Technical Approach
A partitioned approach has been proposed in which the fluid and structure equations of motion are solved in separate domain-specific solvers and the coupling is provided by an interface. This helps to exchange information between the two solvers via relevant physical variables and mass/momentum/energy conservation at the physical interface of the two solvers (shown in Figure 1). The advantage of this approach is that available solvers for these two separate domains, which have been verified and validated in their specific problem domains, can be used. While the concept appears quite straightforward and simple, there are two major research questions: (1) how to update mesh in each computational domain when there is change in interface and (2) how to determine connectivity for information exchange between structured and unstructured mesh. Both research questions can be addressed by the overall workflow shown in Figure 1.
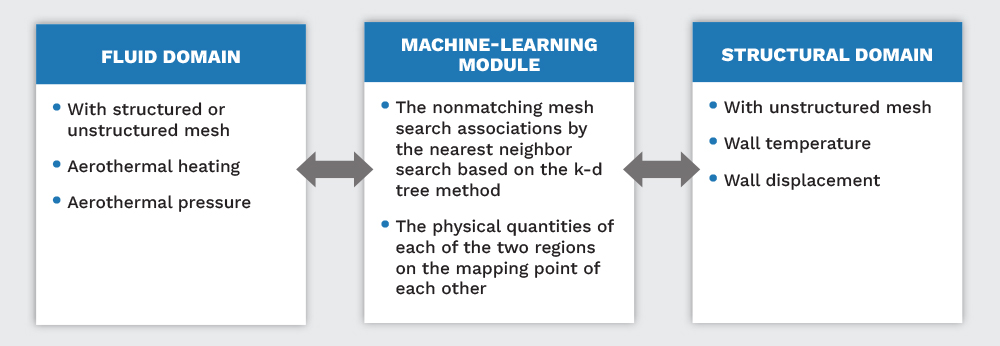
Figure 1. Details of the Interface Methodology (Source: R. Acharya).
Starting with the structured grid and once converged with the stipulated timesteps, the required data for the unstructured grid solver is communicated via the interface and by utilizing the k-d tree nearest neighbor (NN) search algorithm. This method utilizes matrices to approximate the node locations on the new mesh. There are two possibilities for the interface: (1) surface regression (due to processes such as ablation, weather erosion, spallation, etc.) and (2) surface deformation (due to the aerodynamic forces exerted on the surface). Each of these affects the interface between the fluid and structural domains; therefore, the grid deformation of the fluid-structure interface must be determined. If there is no structural deformation that could affect the flow, then the next timestep will be run on the same mesh. This will allow the program to save time by not having to unnecessarily convert the mesh file. In either case, the total grid count in the fluid or solid computational domains will not alter—only the grid will be adapted based upon structural deformations due to mass loss and/or thermo-structural response of the solid. This workflow is shown in Figure 2.
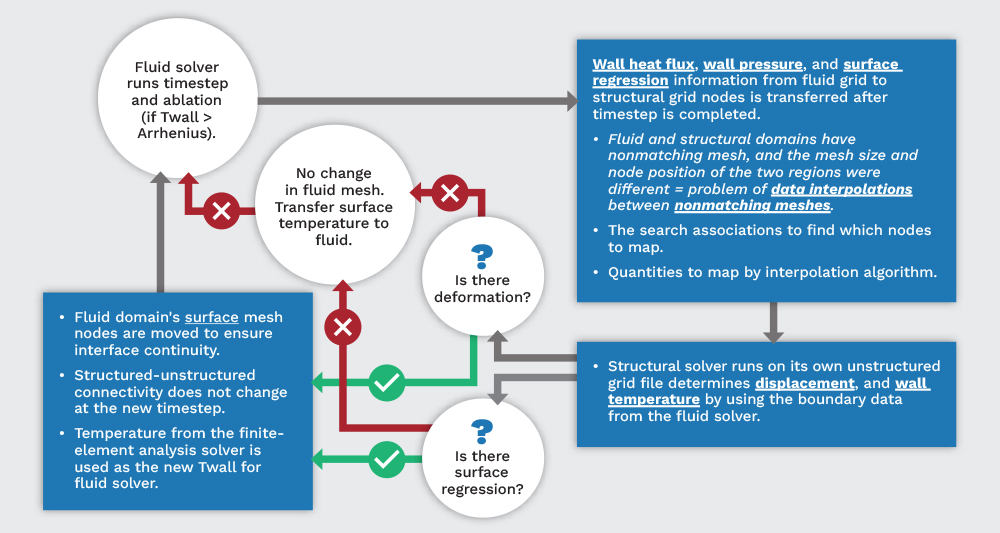
Figure 2. Decision Tree for Mesh Updates in the Fluid Domain (Source: R. Acharya).
k-d Tree Search Algorithm
A structured (corresponding to the fluid solver) mesh and an unstructured (corresponding to the structural solver) mesh are likely to have nonmatching points at the interface between the fluid and structural domains. Therefore, an NN search algorithm is implemented to find the respective mesh points for information exchange. An NN search, a form of a proximity search, is the optimization problem of finding the point in each set closest (or most similar) to a given point. Mathematically, the NN search problem is defined as follows: given a set S of points in a space M and a query point q ∈ M, find the closest point in S to q. M is represented as the d-dimensional vector space where dissimilarity is measured using a distance. Although the distance can be any metric measure, a standard Euclidean distance is used in this work.
Neighbors-based methods are known as nongeneralizing ML methods since they simply “remember” all data transformed into a fast-indexing structure like a k-d tree. A direct generalization of this problem is a k-NN search, where k closest points are found. Despite its simplicity, the NN technique has been successful in many classification and regression problems. Being a nonparametric method, it is often successful in classification situations where the decision boundary is very irregular. Figure 3 shows a schematic description of a k-d tree method.
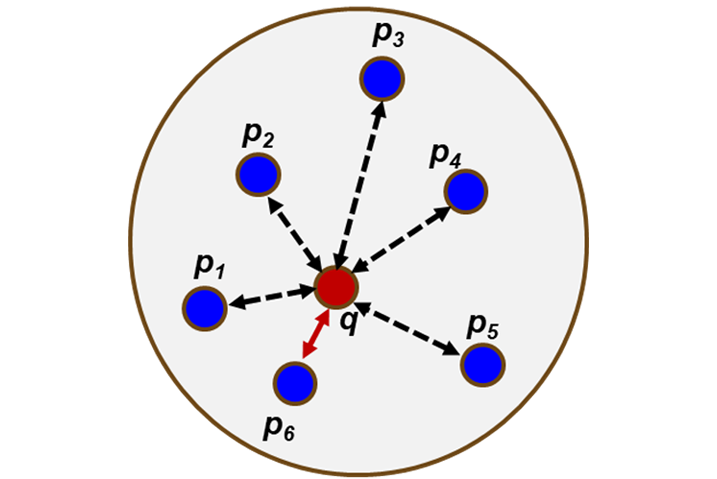
Figure 3. Schematic Description of a k-d Tree Method (Source: R. Acharya).
As shown in the figure, a search is performed to find the NN of point q. There are multiple points in the neighborhood of point q from p1 to p6. Standard Euclidean distance from point q to each pi is calculated, and the point at minimum distance from point q is selected as the NN. In this work, this technique has been expanded to include a two-way search in a two-dimensional (2-D) space, as the fluid-structure interface is a 2-D surface.
Results and Discussion
The first demonstration of this approach is shown in Figure 4, where the fluid domain is on the left side and structural or solid side is on the right side of the interface between the two domains. The X’s represent structured grid nodes, whereas the green dots represent unstructured grid nodes. The red lines connect the nodes on the fluid and solid structure nodes closest to the interface and determine node pairs for data exchange.
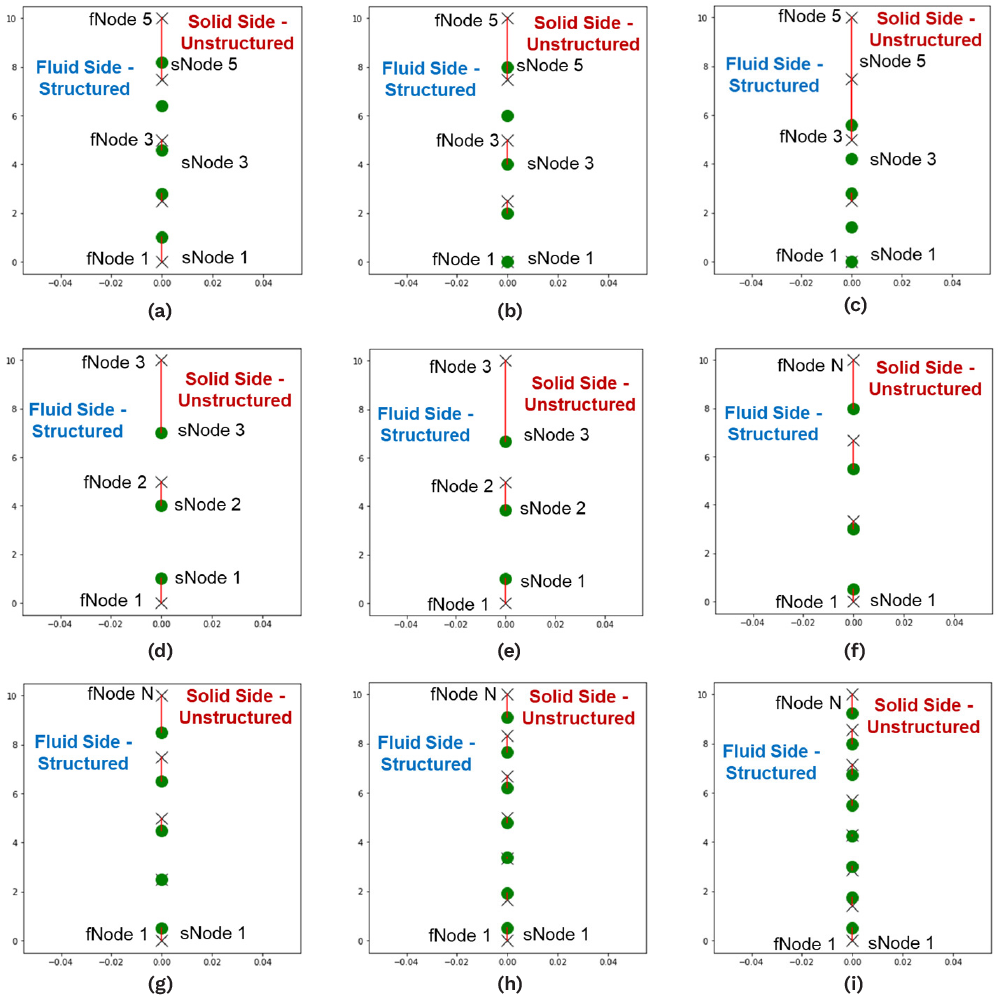
Figure 4. Determining Node Pairs for Data Exchange at the Fluid-Solid Interface (Source: R. Acharya).
Figure 4a shows the section of the interface with five nodes on the fluid and solid sides with 1:1 correspondence. Figures 4b–c show that when the solid nodes move due to expansion, the algorithm still finds the nearest fluid nodes and maintains connectivity for data exchange. Figures 4d–i show that when more nodes are added on either fluid or solid sides, the algorithm still finds the NNs. However, there are equal number of nodes from both fluid and solid sides in these cases. Figure 5 shows how the algorithm connects the nodes of the nonmatching meshes. When nodes are constant but the unstructured nodes move due to expansion, the algorithm still finds the nearest structured nodes. This represents the fluid domain. As with the earlier case, there is 1:1 correspondence between fluid and solid nodes.

Figure 5. Demonstration of Dynamic Interface for a Surface Mesh Interface (Source: R. Acharya).
Figure 6 shows how the algorithm connects the nodes of the nonmatching meshes. The circle represents a cross section of a circular cylinder subjected to shock heating due to supersonic crossflow. The blue dots represent fluid-structured grid nodes. Even though many flow solvers are unstructured solvers near the surface, it is customary to use a quadrilateral mesh to resolve the boundary layer. The orange dots represent solid, unstructured grid nodes. The black lines connect the nodes on the fluid and structure nodes closest to the interface. The cross section of the cylinder is replicated in the python interface.
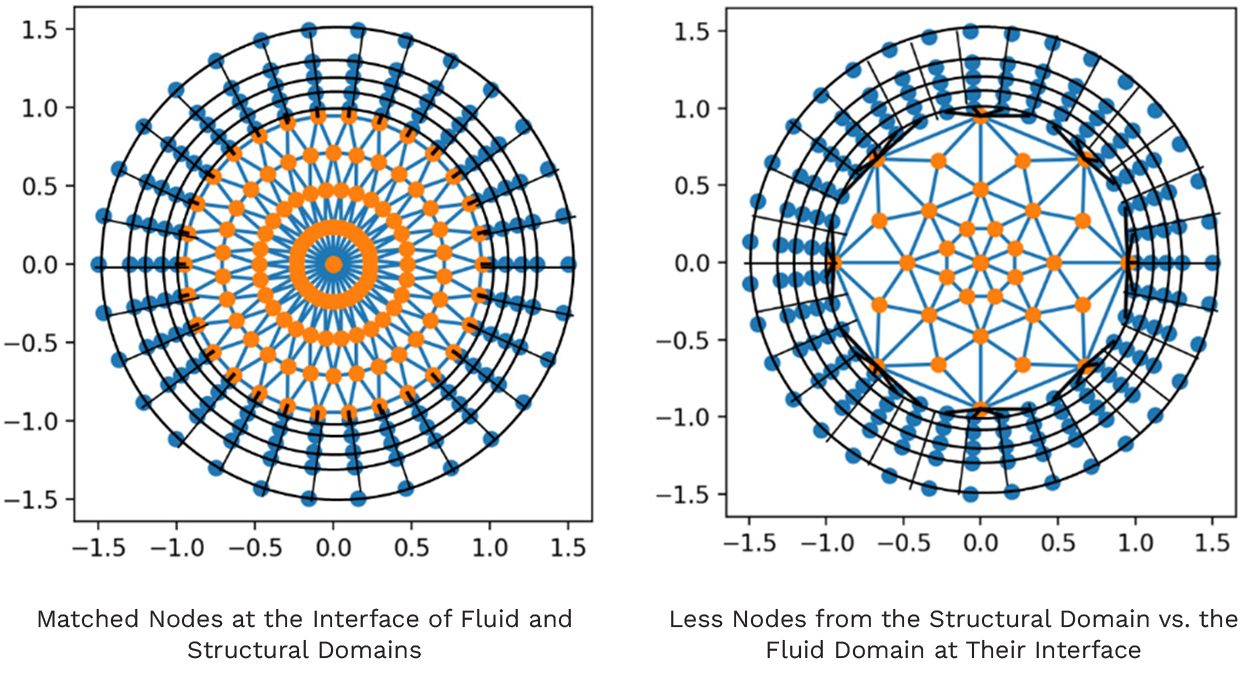
Figure 6. Dynamic Interface Identifying Matching Nodes at the Interface for Data Exchange Between Structured and Unstructured Mesh (Source: R. Acharya).
In Figure 6a, the nodes at the interface between fluid and solid sides have 1:1 correspondence. However, in Figure 6b, the node count from the solid side is significantly lower than the fluid side node count at the fluid-structure interface. The k-d-tree-based data exchange code can find the information exchange nodes in both cases. This is trivial when the fluid and structural side mesh match at the interface; but it is encouraging to note that the algorithm is also successful when different mesh densities on the fluid and solid sides are used (as shown in Figure 6b). Such a capability is possible even if the solid side mesh count is significantly less than the fluid side mesh count on the interface, as shown in Figures 7a–d, or when the mesh count on the fluid side of the interface varies, as shown in Figure 8.
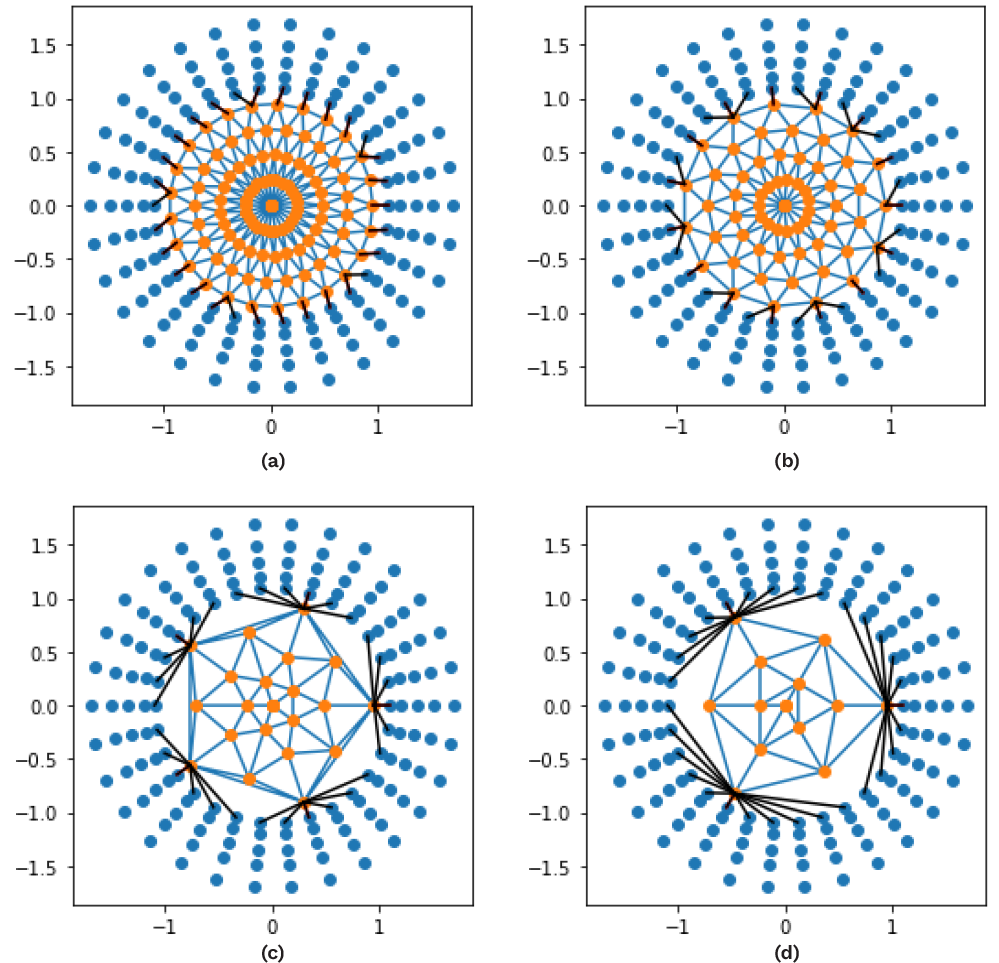
Figure 7. Dynamic Interface Identifying Matching Nodes at the Interface for Data Exchange Between Structured and Unstructured Mesh With Different Mesh Count on the Solid Side (Source: R. Acharya).
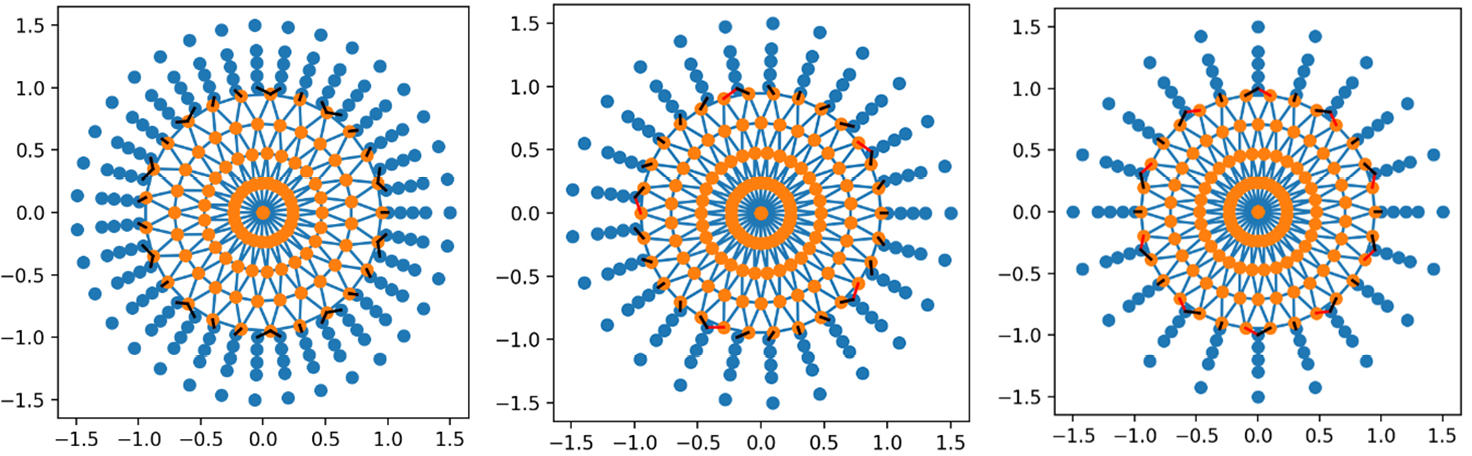
Figure 8. Dynamic Interface Identifying Matching Nodes at the Interface for Data Exchange Between Structured and Unstructured Mesh With Different Mesh Count on the Fluid Side (Source: R. Acharya).
These results demonstrate that the dynamic interface code enables the following:
- Both fluid and structure mesh do not need to match at the interface—they can be arbitrary.
- A robust dynamic interface is significantly greater than simple mesh overlay with respect to computational cost and accuracy.
The dynamic interface data exchange code is tested when the cylinder deforms from a circular cross section to an elliptical shape. Due to such deformation, the nodes on the solid domain move at the interface (the mesh count remains constant), and the fluid mesh moves accordingly, as shown in Figure 9. The deformation of the cylinder does not affect the connectivity between the fluid and solid mesh at the interface between the two domains. Deformation of cylinder does not affect the fluid-structure node connectivity for the case when the number of mesh count remains constant. However, it is not a constraint for this methodology, as shown in Figure 10.
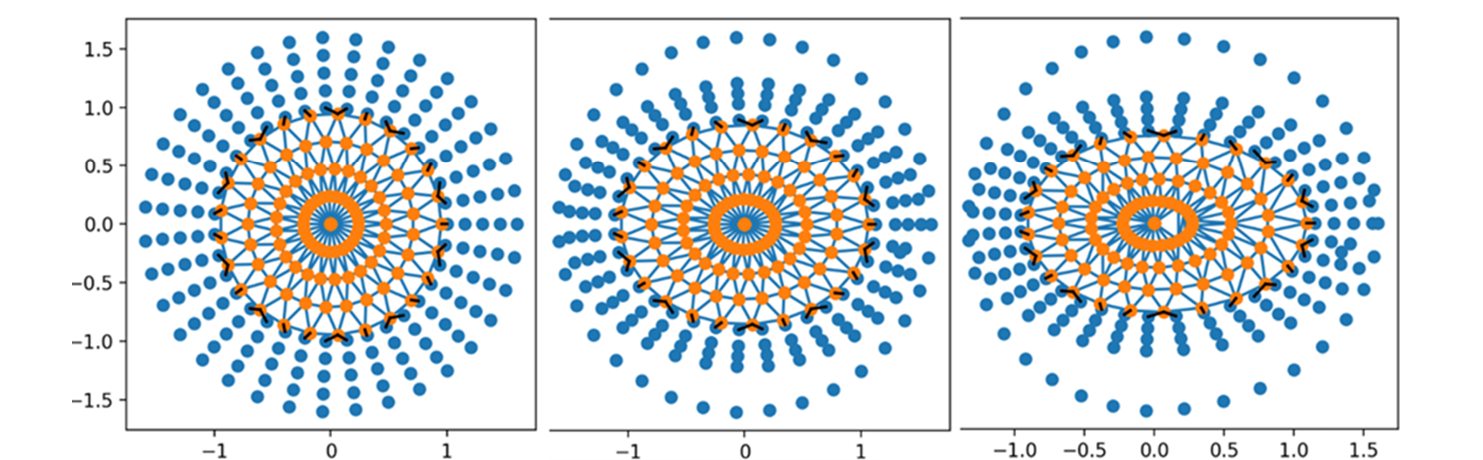
Figure 9. Dynamic Identification of Matching Nodes at the Fluid and Structure Interface When the Cylinder Deforms (Source: R. Acharya).
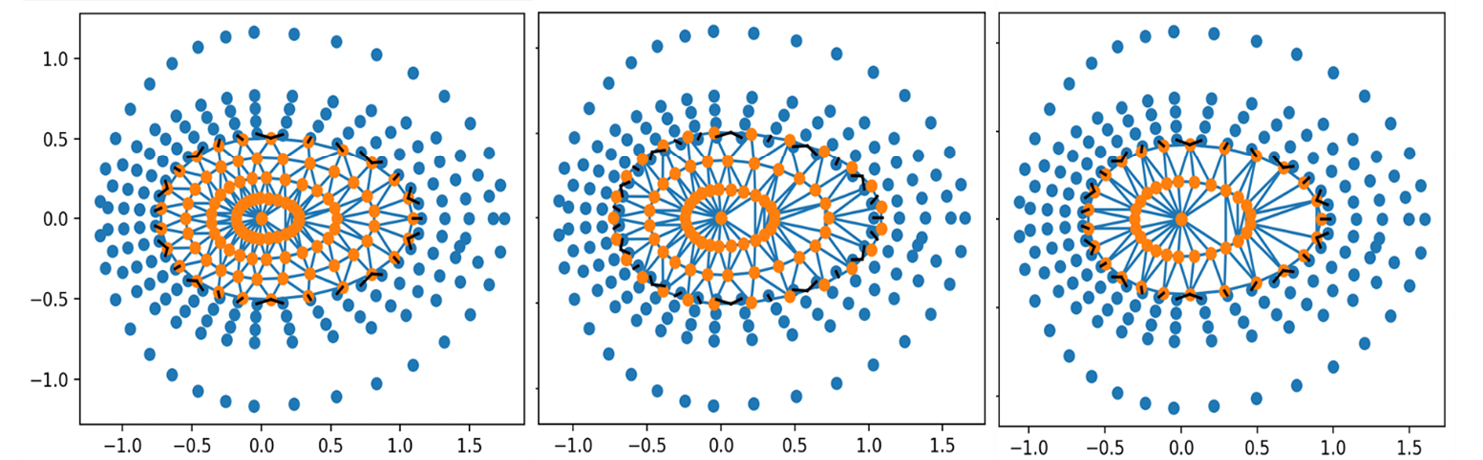
Figure 10. Dynamic Identification of Matching Nodes at the Fluid and Solid Interface When the Cylinder Ablates and Deforms (Source: R. Acharya).
The dynamic interface data exchange code is then tested when the cylinder ablates and deforms from a circular cross section to an elliptical shape. Due to this ablation, the number of mesh nodes from the structural domain at the fluid-structure interface reduces, while deformation causes the nodes to move from their original locations. The fluid mesh is reorganized to occupy the newly generated fluid volume due to the combined ablation deformation process, as shown in Figure 10. Despite the combined ablation and deformation, the algorithm successfully identifies the nodes in fluid and structural domains where data exchange must occur. Such connectivity is maintained between the fluid and structural mesh at the interface between the two domains. Surface regression of the cylinder requires change in the fluid-structure interface connectivity as the mesh count on the interface from the solid side changes. Two-way connectivity can be readily determined with the capability presented in this work, as shown in Figure 10.
In these results, the cylinder’s ablation and deformation are shown to be symmetrical around the streamwise direction—this is not a condition of the algorithm but rather a simplification made for demonstration purposes.
Conclusions
Results from the dynamically coupled interface utilizing a tree-based algorithm show how displacement-and/or ablation-induced surface regression can enable nonmatching mesh on the computational domains on the fluid and structural sides when the mesh size and node position of the two domains are different and dynamically evolving. The tree-based search algorithm performs associations to find the mesh nodes from both domains at the interface and data interpolations between nonmatching meshes for the quantities to map via the interpolation algorithm. This capability can be utilized to determine the 3-D, transient, thermo-structural response of the hypersonic vehicle during its flight. The dynamically coupled codes can provide higher fidelity results in modelling the interdisciplinary thermo-physico-chemical interactions compared to each separately simulated process, and their effects can translate to the other offline code.
Biography
Ragini Acharya is an associate professor in the Mechanical, Aerospace, and Biomedical Engineering Department at the University of Tennessee Space Institute. With over a decade of experience in the aerospace and defense industry, she has been the principal investigator/coinvestigator on hypersonic and propulsion technologies, reacting flow modelling and computations, and uncertainty quantification method development. She coauthored two best-selling, graduate-level textbooks on turbulent and mulitphase combustion; wrote over 50 technical articles in peer-reviewed publications and technical conferences; and received numerous awards. She is an American Institute of Aeronautics and Astronautics (AIAA) Associate Fellow, a member of the Advisory Board National Space and Missile Materials Symposium, and chair of the AIAA High-Speed Air Breathing Propulsion Technical Committee. Dr. Ragini Acharya holds a Ph.D. in mechanical engineering from The Pennsylvania State University.